式の展開までは簡単だったけど、どうも因数分解はわからない問題に出会い嫌になった。

因数分解なんて、なんでこんなことやるのか面倒くさい。

そもそも因数分解などできなくても将来困ることなどない。

でも、こんな基礎的なことができない自分はやはり頭悪いのではないだろうか

文字の羅列を見ただけで虫唾がはしる自分がなさけない。

安心してください。

因数分解はたった３つの道具を使いこなせれば９〇％以上（殆ど）の問題は解けます。

非常にいやらしい特殊な因数分解は特別にあとから練れれば完全制覇も夢ではありません。

ですから、この３つの道具を徹底的に理解しパターンとして見抜ける眼力を鍛えれば因数分解ほど楽な単元はありません。

では早速、道具の１つ目　　【①共通因数くくりだし法】

　これは簡単すぎるかもしれませんが、しっかり理解してできるようになってください。

［例題］

　６abcwyz＋4abxzー8abyz  を因数分解してください。

　上記の式は３つの項でできていて、「各項で共通する文字は括りだす」です。

すると　　　　2･3･ab･cwy･z ＋2･2･ab･x･zー2･2･2･ab･y･z　となり

ジーっと見つめると　2、ab、z　が共通しているから

　2abz(3cwy＋2xー4y)　が答えでした。

２つ目、ここが重要です【②完全平方とな関係】

　　ここが、特に重要で２つの要素が含まれていますが征服すべき道具です。

   ※　完全平方　

　その上で

　［典型例］

　　だったら、まず前半の３つの項に注目すると完全平方になっているから

ここで、もとに戻して

　文字の順位に整理すると

　この関係は　この後「複２次式の因数分解」「平方根の分母の有利化」をはじめ

あらゆるところで応用され使われるので、たっぷり演習問題をやって計算力をつけておくことが極めて重要です。

そして３つ目　【③たすき掛け】　

　ここは、一般的な式の展開を計算した後の式から、逆に計算前の（　）カッコ付の形に戻す方法です。

　ここは、小学校でならった２桁や３桁の数のかけ算の要領に似ています。つまり、縦書きにして、計算の手順をイメージしやすくする方法です。ですから、ここは慣れることが一番重要です。一応念のため考え方を整理してみます。

まず、式の展開の確認

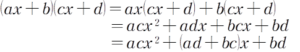
ここで、展開の結果から元の（　　）（　　）に戻るためには左端と右端は簡単に考え付く

パターン１

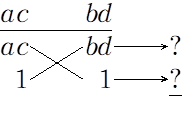
パターン２

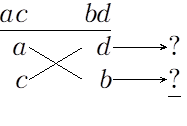
パターン３　　

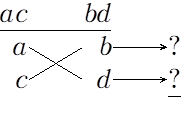
しかし、上記のごとく、いろいろなパターンが思いついてしまうのでど真ん中の係数に合致する場合を探さなければならないのは面倒くさい。

　上記でいうとパターン３のときが　展開式のど真ん中の係数になるので、３パターンまで実験する必要がある。

　　要は、たすき掛けは「面倒です！」でも「慣れてやるしかない！」ということです。

これがなかなかなじめず数学嫌いになるきっかけになったりしますが・・・でも小学校の時の気分に立ち返ってやってみて欲しいのです。

　やるうちにいつの間にか簡単にパターンが見えてくるようになります。

そして、いわゆる受験をふくめ試験で出会う因数分解のほとんどがこの【①共通因数括りだし】【②完全平方とな関係】【③たすき掛け】で解けてしまう（もちろん組み合わさっている）ということに注目してほしいのです。

　残りの数パーセントの特殊因数分解は、その都度覚えれば大丈夫です。特に3次式の因数分解は理数系受験には必須で覚えていた方が良いですが、あとは滅多に出会いません。

　因数分解といったら【①共通因数括りだし】【②完全平方とな関係】【③たすき掛け】の３つの道具の使い方を身に付ければ大丈夫です。