手順化・自動化によって物事を解明しようとする数学的思考にとって、漠としてとらえにくい命題論理の把握は重要です。
デジタル時代を迎え、ますますこの単元「命題論理」は大切です。
さて、数学の基本はイメージ化をここにも応用すると覚えやすくなります。

今回は「必要条件、十分条件、必要十分条件」についてです。
命題 『 条件P ならば 条件Q である』が真とは、
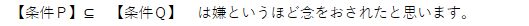
つまり、集合の図(イメージ)として真や偽を把握するとわかりやすく覚えやすかったのでしたね。
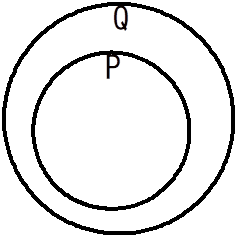
このときのいい方は「条件P=>条件Q」は真実であるでした。
同時に、逆も一緒にイメージで理解してほしいのです。

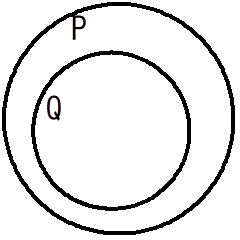
この時のいい方は 「条件Q=>条件P」は真実であるです。
かなり強引ですが次のような表現もできます。「条件P<=条件Q」は真実である。
要は、「ならば」の方向 「=>」か「<=」が、どちらの条件から、どちらの条件に向かっているかが大切です。

つまり、「ならば」の方向 「=>」なのか「<=」なのかどちらで命題が真になるか!
この方向を確認することが重要です。そして、単純なイメージ図(イラスト)
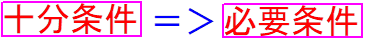
あとは、機械的に当てはめるだけです。
つまり 「左=>右」ならば 左条件が(右にとっての)十分条件。
右条件が(左にとっての)必要条件
逆向きも一緒にイメージ化して覚えておくと忘れにくいです。
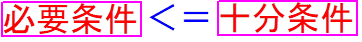
つまり 「左<=右」ならば 右条件が(左にとっての)十分条件。
左条件が(右にとっての)必要条件
じつは、たったこれだけです。

応用問題などで出題されるのは、この真であるための方向が決めにくい問題です。
そう、命題論理には直接関係ない整数問題や不等式などです。
とくにわかりにくいのは「整数の性質」のところをしっかり理解しておかないと困る問題が多いです。「整数の性質(約数・倍数、商余り、不定方程式、n進法、素数問題)」は別の機会に挑戦してください。(ここも面白さ満載ですよ!特に「123456は9の倍数か?など)




コメント