いろいろな物には綺麗なパターンがあります。
※ 木、葉っぱ、波、雪結晶、タンパク質、FXなどなど フラクタルデザインといわれるパターン繰り返しもあります。

このパターンに気付いたら、鬼に金棒。算数・数学における計算でいえば、元は単純パターン。
このパターンが見える様になることが必須です。
あらゆる式はパターンが見抜ければ超簡単な式だらけです。
そしてパターンを見抜くには小さなパターンをカッコ( )でまとめ、文字と置き換えてみる。

カッコはとても重要です。とにかく( )カッコを一まとまりと見做す感覚(ダメなときは文字AとかXとか置換してみる。)が身につけば、たったこれだけで、中学2年~高校1年ぐらいの基礎計算は征服したも同然です。

【中3数学から高校1年数学Ⅰでつまずく典型例で説明します】
※ 完全平方式のパターンが見抜けない。
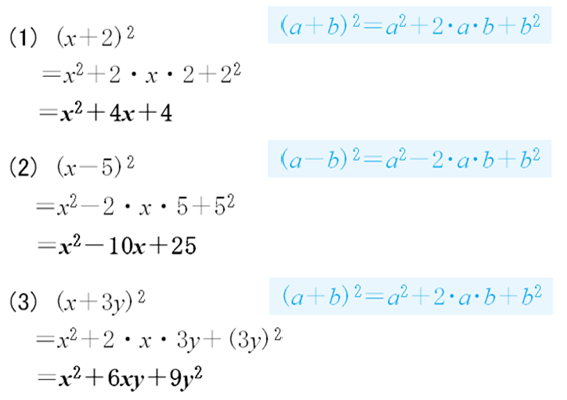
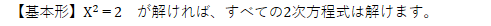
この2次方程式の解は
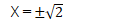
です。

この基本パターンが身についていれば、すべての2次方程式は必ず解けます。
もちろん、解の公式を徹底的に覚えてできる人も多いと思いますがやはり、解の公式そのものも、この基本形で解いただけなので、この基本パターンは見抜けるようにしておいてほしい。
【ちょっと例題】
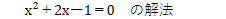
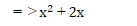
を見た瞬間に
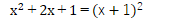
の完全平方式パターンが浮かぶことがポイント
解]与式をちょっと変形して



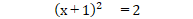
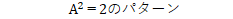
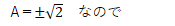
戻して
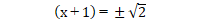
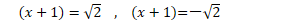
だから
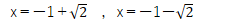
もちろん、解の公式丸暗記で、試験を突破することも重要です。
でも、この完全平方のパターンは、数学Ⅰの平方根の計算や2次関数になると多用されます。
数学Ⅰで2次関数が嫌いな人の大半は、この完全平方パターンが見抜けない場合です。
更には、数学Ⅰ平方根の計算での2重混合で利用されるのも完全平方パターン
そもそも、因数分解における
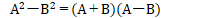
にしても
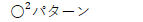
ですから、せめて次のパターンは、しっかり計算パターンとして血肉化して置くこと(覚えておく事)が大切です。
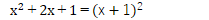
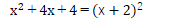
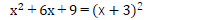
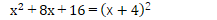
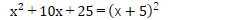
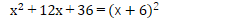
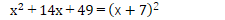
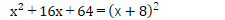
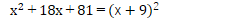
そして、ぜひとも忘れては困るパターンが
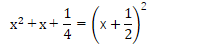
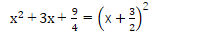
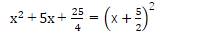
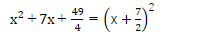
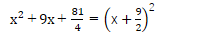
もちろん、次の平方までは是非とも覚えておいてほしいものです。
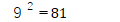
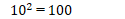
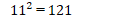
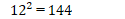
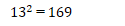
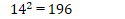
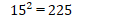
世界は、基本パターンとその繰り返しでできている。




コメント